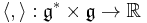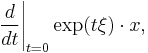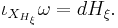Moment map
In mathematics, specifically in symplectic geometry, the momentum map (or moment map) is a tool associated with a Hamiltonian action of a Lie group on a symplectic manifold, used to construct conserved quantities for the action. The moment map generalizes the classical notions of linear and angular momentum. It is an essential ingredient in various constructions of symplectic manifolds, including symplectic (Marsden–Weinstein) quotients, discussed below, and symplectic cuts and sums.
Contents |
Formal definition
Let M be a manifold with symplectic form  . Suppose that a Lie group G acts on M via symplectomorphisms (that is, the action of each g in G preserves
. Suppose that a Lie group G acts on M via symplectomorphisms (that is, the action of each g in G preserves  ). Let
). Let  be the Lie algebra of G,
be the Lie algebra of G, 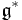 its dual, and
its dual, and
the pairing between the two. Any  in
in  induces a vector field
induces a vector field  on M describing the infinitesimal action of
on M describing the infinitesimal action of  . To be precise, at a point x in M the vector
. To be precise, at a point x in M the vector 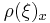 is
is
where  is the exponential map and
is the exponential map and  denotes the G-action on M.[1]. Let
denotes the G-action on M.[1]. Let  denote the contraction of this vector field with
denote the contraction of this vector field with  . Because G acts by symplectomorphisms, it follows that
. Because G acts by symplectomorphisms, it follows that  is closed for all
is closed for all  in
in  .
.
A moment map for the  -action on
-action on 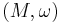 is a map
is a map  such that
such that
for all  in
in  . Here
. Here 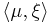 is the function from M to
is the function from M to  defined by
defined by  . The moment map is uniquely defined up to an additive constant of integration.
. The moment map is uniquely defined up to an additive constant of integration.
A moment map is often also required to be G-equivariant, where G acts on 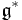 via the coadjoint action. If the group is compact or semisimple, then the constant of integration can always be chosen to make the moment map coadjoint equivariant; however in general the coadjoint action must be modified to make the map equivariant (this is the case for example for the Euclidean group).
via the coadjoint action. If the group is compact or semisimple, then the constant of integration can always be chosen to make the moment map coadjoint equivariant; however in general the coadjoint action must be modified to make the map equivariant (this is the case for example for the Euclidean group).
Hamiltonian group actions
The definition of the moment map requires  to be exact. In practice it is useful to make an even stronger assumption. The
to be exact. In practice it is useful to make an even stronger assumption. The  -action is said to be Hamiltonian if and only if the following conditions hold. First, for every
-action is said to be Hamiltonian if and only if the following conditions hold. First, for every  in
in  the one-form
the one-form  is exact, meaning that it equals
is exact, meaning that it equals  for some smooth function
for some smooth function
If this holds, then one may choose the 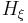 to make the map
to make the map 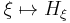 linear. The second requirement for the
linear. The second requirement for the  -action to be Hamiltonian is that the map
-action to be Hamiltonian is that the map 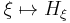 be a Lie algebra homomorphism from
be a Lie algebra homomorphism from  to the algebra of smooth functions on M under the Poisson bracket.
to the algebra of smooth functions on M under the Poisson bracket.
If the action of G on 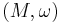 is Hamiltonian in this sense, then a moment map is a map
is Hamiltonian in this sense, then a moment map is a map  such that writing
such that writing  defines a Lie algebra homomorphism
defines a Lie algebra homomorphism 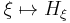 satisfying
satisfying 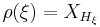 . Here
. Here  is the vector field of the Hamiltonian
is the vector field of the Hamiltonian 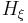 , defined by
, defined by
Examples
In the case of a Hamiltonian action of the circle  , the Lie algebra dual
, the Lie algebra dual 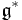 is naturally identified with
is naturally identified with  , and the moment map is simply the Hamiltonian function that generates the circle action.
, and the moment map is simply the Hamiltonian function that generates the circle action.
Another classical case occurs when M is the cotangent bundle of 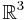 and G is the Euclidean group generated by rotations and translations. That is, G is a six-dimensional group, the semidirect product of
and G is the Euclidean group generated by rotations and translations. That is, G is a six-dimensional group, the semidirect product of 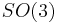 and
and 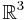 . The six components of the moment map are then the three angular momenta and the three linear momenta.
. The six components of the moment map are then the three angular momenta and the three linear momenta.
Symplectic quotients
Suppose that the action of a compact Lie group G on the symplectic manifold 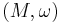 is Hamiltonian, as defined above, with moment map
is Hamiltonian, as defined above, with moment map  . From the Hamiltonian condition it follows that
. From the Hamiltonian condition it follows that 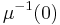 is invariant under G.
is invariant under G.
Assume now that 0 is a regular value of  and that G acts freely and properly on
and that G acts freely and properly on 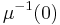 . Thus
. Thus 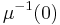 and its quotient
and its quotient 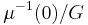 are both manifolds. The quotient inherits a symplectic form from M; that is, there is a unique symplectic form on the quotient whose pullback to
are both manifolds. The quotient inherits a symplectic form from M; that is, there is a unique symplectic form on the quotient whose pullback to 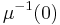 equals the pullback of
equals the pullback of  to
to 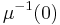 . Thus the quotient is a symplectic manifold, called the Marsden–Weinstein quotient, symplectic quotient or symplectic reduction of M by G and is denoted
. Thus the quotient is a symplectic manifold, called the Marsden–Weinstein quotient, symplectic quotient or symplectic reduction of M by G and is denoted 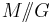 . Its dimension equals the dimension of M minus twice the dimension of G.
. Its dimension equals the dimension of M minus twice the dimension of G.
See also
Notes
- ^ The vector field
 is called sometimes the Killing vector field relative to the action of the one-parameter subgroup generated by
is called sometimes the Killing vector field relative to the action of the one-parameter subgroup generated by  . See, for instance, (Choquet-Bruhat & DeWitt-Morette 1977)
. See, for instance, (Choquet-Bruhat & DeWitt-Morette 1977)
References
- J.-M. Souriau, Structure des systèmes dynamiques, Maîtrises de mathématiques, Dunod, Paris, 1970. ISSN 0750-2435.
- S. K. Donaldson and P. B. Kronheimer, The Geometry of Four-Manifolds, Oxford Science Publications, 1990. ISBN 0-19-850269-9.
- Dusa McDuff and Dietmar Salamon, Introduction to Symplectic Topology, Oxford Science Publications, 1998. ISBN 0-19-850451-9.
- Choquet-Bruhat, Yvonne; DeWitt-Morette, Cécile (1977), Analysis, Manifolds and Physics, Amsterdam: Elsevier, ISBN 978-0720404944